How does ExcelCompiler work?

Introduction

ExcelCompiler (formerly FastMC) is a software tool developed and published by Ogee Group LLC to translate a cell formula, such as “=SUM(A1:A10)”, into a VBA procedure performing the same calculation. Excel Compiler will also translate the formulas of all necessary precedent cells that determine a compiled cell’s value. When any random number “RAND()” is encountered, Excel Compiler generates a procedure for Monte Carlo simulations.

Potential uses of Excel Compiler include:

• Simplifying complex spreadsheets by replacing certain groups of cells with VBA functions.
• Hiding specific proprietary calculations inside VBA functions (combined with password protection of VBA modules).
• Hiding specific proprietary calculations inside VBA functions (combined with password protection of VBA modules).

A simple example

Any cell in an Excel spreadsheet can either have its own, independent value, or be a function of several input values from several precedent cells. The values in these cells in turn may be both the input and output of several functions in other cells. Take the following sequence of cell functions as an example:

Figure 1: a simple three-step calculation

Here, A1 is a single input cell, C1 is the output cell, and B1 is an intermediate calculation step. Accordingly, Excel Compiler would write a VBA function that takes a single input parameter with a default value of 2, replicates the successive calculation steps, and returns the result:

Function MyCell(Optional R1C1 = 2#)
  …
  cells.Cell(0) = R1C1
  cells.Cell(1) = R1C1 + 1
  cells.Cell(2) = cells.Cell(1) ^ 2

  MyCell = cells.Cell(2)
End Function

Directed graphs

Figure 2: complex hierarchy of interdependent cells

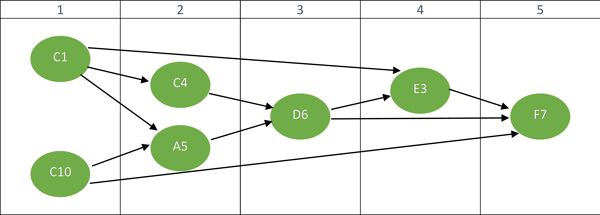
Here, finding the successive calculation steps from input values to the final output value is not immediate (give it a try!). In yet more complex scenarios, this task can prove quite difficult for a human being. To help find these steps, Excel provides the “Trace Precedents” and “Trace Dependents” commands in its “Formulas” tab.

In order to write a VBA procedure that replicates the calculation of the output cell with its intermediate steps in correct order, Excel Compiler relies on the concept of directed graph. In mathematics, a directed graph is a set of nodes connected by edges (i.e. lines) that have a direction. Here, nodes are cell values, and directed edges represent formula dependencies. This is the directed graph corresponding to our last example:

Figure 3: directed graph corresponding to Fig. 2

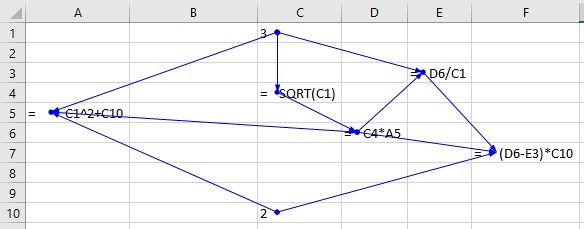
Note that a directed graph only represents the directional flow of calculation steps in an abstract way. It does not solve the problem of finding the logical order of the steps from input to final output. To do so, Excel Compiler deploys a proprietary algorithm [Patent Pending] that assigns a rank to each cell. Cells of lowest rank must be computed first, then cells of second lowest rank, and so on until the final output cell which has the highest rank. This ranking algorithm provides an orderly flow of calculation that respects the dependencies between nodes. In our example:

Figure 4: directed graph after ranking

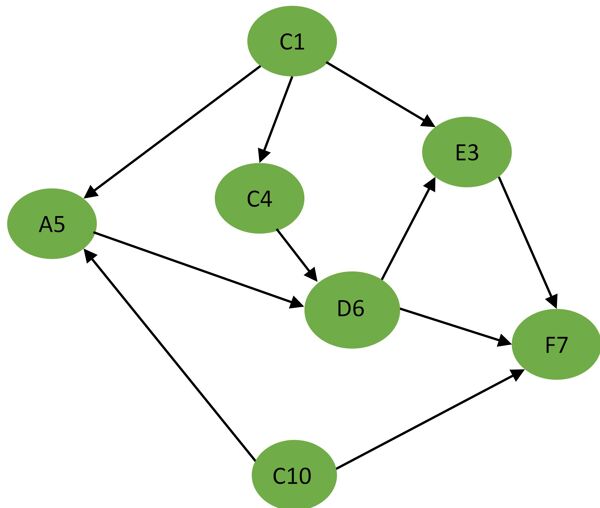
Cells are then “bucketed” by rank, where each bucket corresponds to a stage in the sequence of calculations. Within any given bucket, the particular sub-order of calculation does not matter. In our example, C10 may be calculated before C1, and A5 may be calculated before C4; however, both C1 and C10 must be calculated before C4 and A5.

Graph theory is particularly interested in cycles. In Excel, cycles are known as circular references: for example, if the formula for cell A1 is “=B1” and vice-versa. Circular references are typically disallowed and Excel Compiler would fail in their presence.

Code generation

After ranking the cells, Excel Compiler transcribes the individual cell functions into VBA code. Each function can take as its input the values of lower-ranked cells, until the final output in this sequence of calculations is produced. The full code for Example 1 is given below:

Function MyCell(Optional R1C1 = 2#)
    Dim cells As New CellSet, c As String
    c = "R1C1 R1C2 result"
    cells.Define c

    cells.Cell(0) = R1C1
    cells.Cell(1) = R1C1 + 1
    cells.Cell(2) = cells.Cell(1) ^ 2

    MyCell = cells.Cell(2)
End Function

Note that Excel Compiler uses the R1C1 reference style to label cells. Here we have a function that takes a single input parameter corresponding to cell R1C1 (A1), creates a data structure for all three cells needed for the calculation (the graph nodes), and then performs the successive calculations before returning the result.

Additionally, Excel Compiler can deal with cell ranges which require additional initialization instructions, and will automatically switch to Monte Carlo mode whenever a random number (“RAND()”) is encountered in any cell formula.

In Monte Carlo mode, Excel Compiler embeds the relevant calculation instructions within a loop. Each step of the loop simulates a new value of the output cell which contributes to the average. Continuing Example 1, if we replace the value of A1 with the formula “=RAND()” and run Excel Compiler, we obtain the following code:

Sub MyCell(nSim As Long)
    Dim i As Long, avg As Double, cells As New CellSet, t As Single, c As String
    t = Timer
    c = "R1C1 R1C2 result"
    cells.Define c

    For i = 1 To nSim
        cells.Cell(0) = Rnd
        cells.Cell(1) = cells.Cell(0) + 1
        cells.Cell(2) = cells.Cell(1) ^ 2

        avg = avg + cells.Cell(2) / nSim
    Next i

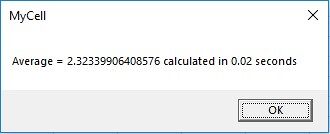
    MsgBox "Average = " & avg & " calculated in " & Format(Timer - t, "Standard") & " seconds", vbOKOnly, "MyCell"

End Sub

We can see that the generated code is similar, but with some important differences. First, in Monte Carlo mode, Excel Compiler creates a subroutine rather than a function. This is because large Monte Carlo simulations can take a long time to calculate and should not be invoked from a spreadsheet function, especially when the spreadsheet is in automatic calculation mode.

Second, the calculation steps are now embedded in a for loop whose number of iterations is passed to the subroutine as a parameter (nSims). An additional variable (avg) keeps track of the average simulated value. Finally, once the loop is completed, the average value is displayed in a dialog box together with the calculation time:

Figure 5: message displaying Monte-Carlo simulation average